|
Are Crisps Overweight?
Weighing the Crisps
You will need 25 bags of crisps, and an accurate weighing
machine.
We shall weigh 25 bags of crisps to see how much they vary.
You will record the results in Table 6 on page R1.
- Weigh the first bag and its contents. Write the
weight to the nearest gram in column 1.
- Empty it and weigh the empty bag. Record this
weight to the nearest gram.
- Subtract the weight of the bag to find the NET
WEIGHT of crisps. Record this in column 2.
- Weigh the other 24 full bags (unopened) recording
the results in column 1.
Assume that each empty bag weighs the same as the first bag.
- Work out the net weight of crisps in each bag.
Write this in column 2.
- What are the stated 'Minimum
contents' of each packet? Write
this above Table 6.
We can find out how much overweight each packet is:
Overweight = (Net weight) - (Minimum contents)
- Work out how many grams overweight each packet
is. Record the results in column 3. Remember to use + and
- signs, as appropriate.
The Crisp Chart
You will need a sheet of graph paper.
- Draw a quality control chart like the one in Figure 2.
You may need to use different numbers on the vertical
axis. (Leave room for the bars on the right of the chart,
but do not draw them yet.)
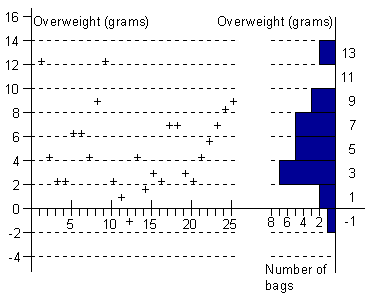
Figure 2 - Quality control chart showing the
amount over weight of 25 packets of crisps.
Use your quality control chart to answer these questions. (The
answers from Figure 2 are shown in
brackets.)
- How many underweight bags were there? (1)
- How many bags were more than 2 grams overweight?
(22)
- How many bags were overweight? (24)
- What proportion of bags were overweight? (24/25)
- What was the range of weights of bags of crisps?
(- 1 g to 12.5 g, a range of 13.5 g)
In questions g, h and i, ignore the five heaviest and the five
lightest bags. This leaves 15 bags.
- What is the heaviest weight among these 15 bags?
(7,5 g)
- What is the lightest weight among these 15 bags?
(2. 5 g)
- What is the range of weights among these 15 bags?
(5 g)
15 bags out of all the 25 bags is:
15/25 x 100/1%
of the bags = 60% of the bags
Copy out the following sentence, filling in the missing
figure.
- *The range of weight of the middle 60% of the
bags is _____ .
Average Contents of Crisp Packets
In the quality control chart in Figure 2,
two bags were between 0 and 2 grams overweight. The mean
overweight of those two bags is 1 gram.
- Which bar on the right of the chart represents
these two bags?
The bars together make up a HISTOGRAM.
- Take out the quality control chart that you drew
of the crisps. On it draw a histogram from your own
figures. Arrange it like the one in Figure 2.
One way of finding the mean overweight of the packets of
crisps is to add up the overweights and divide by the number of
packets.
Can you think of a quicker way? (Hint: Use the
histogram.)
- Find the mean overweight by the quickest way you
can.

*Give-away Weights
A firm of crisp manufacturers weighed 1000 bags of crisps. The
minimum contents of a bag were stated as 24.5 grams. The
overweights of the bags are recorded in Table 7 on page R1.
The crisp manufacturer uses the words GIVE-AWAY WEIGHT to mean
the excess weight above the declared minimum.
In Table 7 the six heaviest bags are between 12 and 14 grams
overweight.
We estimate the mean overweight of these six bags to be 13
grams.
Why?
The mean overweight is recorded in column 3 of the table.
The give-away weight of the six heaviest bags is 6 x 13g = 78
grams. This is recorded in column 4 of Table 7.
- Complete columns 3 and 4 of Table 7. Some figures
have been put in for you.
- What is the total give-away weight of the 1000
bags?
- Calculate the mean give-away weight of a bag.
- Calculate the mean weight of a bag. (The declared
minimum weight of each bag is 24.5 grams.)
- Compare the mean weight of a bag with the mean
weight of a bag from your own sample in Section D3.
- Why does the manufacturer allow such a large
give-away weight?
|