|
Brief Description
This unit introduces the capture-recapture method of
estimating population sizes and uses this to look at some of the
problems of estimating and the properties of estimators.
Design Time: About 4 hours.
Aims and Objectives
On completion of this unit pupils should be able to estimate
populations using the capture-recapture method which is used in
biology. They will have practised this through simple examples
using proportion and harder examples using a formula. They should
be more aware of the effect of sample size and various practical
problems on the accuracy of estimates. They should appreciate
that any estimate is liable to be inaccurate and that there is
variability amongst estimates.
Prerequisites
Pupils will be assumed to have some basic knowledge of
proportion, to be able to manipulate simple fractions and cancel
common factors, and substitute into and evaluate a simple
fractional formula. They should also be able to work out simple
means.
Equipment and Planning
Several hundred small beads or cubes of different colours are
needed in Section C. Sampling bottles could be used if
available. Section D1 needs prior planning. Pupils will
work individually except in Section C where small groups
are required.
Detailed Notes
Section A
It is hoped that a class discussion will show that the problem
we are dealing with is real and will help children to see some of
the difficulties involved.
Some of the topics can be followed up by reference to articles
on 'The Plight of Whales' in Statistics: A Guide to the
Unknown (ed. J. Tanur) and 'Estimating the size of Wildlife
Populations' in Exploring Data (ed. F. Mosteller, et al.).
Methods other than capture-recapture for the whale, cod or
herring problem involve examining the rate of catching over the
years or an analysis of the age of the fish caught. This can be
deduced from the number of dark bands in the growth rings of the
fishes' scales.
The emphasis on estimating, not counting, is essential.
Counting is impossible and estimates will vary.
Section B
This section spells out the basic principles of the capture-recapture
method. The importance of approximation cannot be overstated.
There are many assumptions made in the use of proportion in the
second catch and some are spelled out in Section D2. It
would be useful in B1 to give specific figures for the
second catch (e.g. a catch of 40 with 11 marked red) and see the
implications of trying to put 11/40 = 1/4
B1
Waiting for one day was necessary to allow the fish to
mix (an important point which should be stressed here, though the
point of waiting is brought up in later questions). This makes it
reasonable to assume that each fish has an equally likely chance
of being caught in the second sample.
The format of Table 1 is used to help pupils see the pattern
of the numbers. Initially we consider a pond where the numbers of
fish is known, since this makes the process easier to visualize
and enables the basic principles to be laid down. There are two
ways of looking at the figures in this table to get an estimating
procedure. One, based on the idea of the proportion of marked
fish in the pool and in the second sample, is spelled out in the
pupil notes between g and h.
The second is to say that the second sample contained, 40/100
of the fish in the pond, so that we expect it to contain, 40/100
of the marked fish, giving the answer 10 as before.
- There are both practical and statistical problems here.
The practical ones will be dealt with in D2. The
statistical ones are:
- It may be numerically impossible to get exactly
the right answer, i.e. in a second sample of 15
where the proportion is 1/4:
x/15 = 1/4
has no solution with x as a whole number.
- The inherent variability in the number of marked
fish caught the second time leads to a number of
different estimates on different occasions.
B2
Here we move from a pond containing a known number of
fish to one where the population is not known.
The same basic principles apply as in B1, and the
number patterns may well be seen from Table 2 in many forms, e.g.
(in algebraic terms) if the table is:
| |
In the pond |
In 2nd sample |
| Marked fish |
c |
r |
| Fish altogether |
N |
s |
Then some will see c/N = r/s.
Others will see or s/N = r/c
or Nr = cs,
or c/r = N/s,
or N/c = s/r
It is this last formula that is followed up in the text.
Figure 1 illustrates the same figures as Table 2 but in a less
abstract way and this may be used to help the weaker pupils who
may find this section slightly difficult. Blank Table 5 on page R1
is used for the worked example in a to d.
Further copies of this blank table can be drawn up to help with
the remaining examples. All examples from e to j
are optional for reinforcement of the pattern. Weaker pupils
might copy the worked example as a guide to the method.
B3
This section brings out the formula more explicitly.
Pupils with a background in more formal algebra may like to let:
c = first sample size (captured)
s = second sample size
r = number of marked fish in the second sample (recaptured)
N = number of fish in the pond
and get the formula N = cs/r.
One way of getting this is shown formally in the text. Other
methods are transformations of the formulae described in B2.
It is better if children see the pattern from the numbers rather
than learn a formula.
More difficult numbers are also introduced to emphasize the
fact that the answers are only estimates and it is sensible to
give estimates to whole numbers only.
- The occurrence of no marked fish in the second example
gives an estimate of an infinitely large number of fish
when using the formula, or intuitively no estimate at all
(except that it is more than the sum of the two samples).
This might happen if the first sample were small compared
with the overall population. When testing this work in
schools, one girl suggested that it would happen if the
marked fish were hiding. This led to an interesting
discussion on whether fish were equally likely to be
caught a second time. This is followed up in Sections D
and E.
- This would happen if the first sample netted all or
nearly all of the fish in the pond. The estimate would be
'about the number of fish captured at first'.
Section C
There are three main points behind the simulation.
- To show the effect of sample sizes on the reliability of
estimates.
- To emphasize the many (sometimes unrealistic) assumptions
made in the capture-recapture process. This point is
taken up again in the next section.
- To show that there can be a considerable range of
estimates, and that a good estimate should have its
distribution centring on the true value with as small a
spread as possible.
Working in small groups, of say
four, is essential here to avoid an important experiment
becoming tedious.
It is suggested that each group has the same number (around
100) of beads in its container for C1 to C4,
and thus groups might 'compete' to see who can achieve
the closest estimate.
There are many ways of arranging this work. C1 and C2
keep the same capture size but change the recapture size. C3
and C4 also keep a constant (but higher) capture size
and change the recapture size. It would be useful if all groups
did two of C1 to C4 and that each of C1
to C4 was done by at least one group. Groups doing C1
and C2 or C3 and C4 would see the
effect of changing the recapture size. Groups doing C1
and C3 or C2 and C4 would see the
effect of changing the capture size.
It is useful to collect and display the class results as a
line chart such as in Figure T1. In this way the effect on the
estimates can clearly be seen.
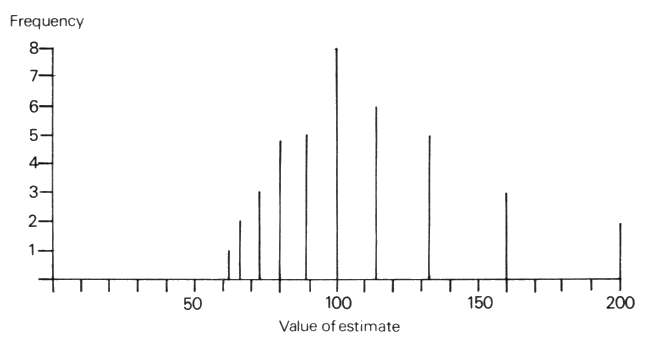
Figure T1 - Estimates based on a capture size of
20, a recapture size of 40
The variation in the size of r is important to show
the considerable degree of variation in estimates, especially for
c = 20.
Some groups might like to draw one or two line charts to show
the distribution of their estimates around the true value.
Section D
D1
The practicality of this example depends on the nature
of the school. It does pose organizational difficulties, but if
it can be attempted it emphasizes very well many assumptions made
and problems faced in actually using the capture-recapture method.
Two ways are suggested for marking pupils.
- The sampler gives the sampled pupils a coloured counter (if
more than one group does the sampling, each could use a
different colour). The recapture sampler will go out the
second day (or later the same day) to ask how many of his
sample have his coloured counter.
- On the first day the sampler asks the sampled pupil his
name and form. On the second day another sampler does
exactly the same. Those on both lists are the recaptured
ones.
It is important that different pupils go out on two successive
days and that some randomization of interviewing is attempted.
This may be done by randomizing the position to which the
interviewers go each day. Pupils should be warned not to
interview only those of the same sex, same age group, etc.
Sample sizes should be a reasonable proportion of the total
population being sampled in order to get a reasonable number of 'recaptures'.
If the biology department has a school pond or does a capture-recapture
experiment elsewhere, this could take the place of D1.
D2
This section is designed to get the children thinking
about the practical difficulties involved, and the ways that the
simple mathematical model used does not reflect reality. Answers
to some of these questions are qualitative - along the lines of:
'This will make the estimates a little less reliable and they
will tend to be underestimates.'
- Other assumptions made, but not specifically mentioned,
are that we are able to capture a reasonable proportion
of the whole population at the first attempt, and that
this is a random sample.
Points which affect the assumptions include the following:
Birth, death, immigration and emigration processes will change
the population.
Any shoaling effect of the fish would upset this assumption.
There may be many reasons for the third assumption to be
untrue. Marked fish may have been harmed in the marking. The fact
that they have been caught once may show that they are more
likely to be caught anyway or that they will be more wary next
time. If the sampling is done at the same place each time then,
unless there is complete mixing, those fish living in
inaccessible places won't be caught; and so on. Other problems
may be connected with the actual marking and finding the marks on
the second sample.
Section E
This section can be treated as an exercise to see whether or
not the ideas of the previous section have been assimilated.
E1
Reliability is poor because of the small number of
marked fish in the second sample. A more reliable estimate would
be obtained by taking either a larger first sample or a larger
second sample.
E2
Setting traps in the same place each time means you are
more likely to catch the same squirrels and not likely to catch
squirrels in a different part of the wood, so the original
estimate is an underestimate.
E3
Over two years there would be deaths and migration of
marked squirrels so that at the second sampling the true number
of marked squirrels is less than those originally marked. This
means that we overestimate the number of squirrels in the wood.
The effect of the hunters is in the same direction.
E4
A number of marked whales in the second sample would be
counted as unmarked. This leads to an overestimate of the
population. With the growth of conservation movements such as 'Green
Peace' the problem of assessing the numbers of whales is likely
to become a more emotive issue.
Answers
| B1 |
a |
The number of fish in the pond and the
number of fish in the second sample respectively. |
| |
c |
1/5 |
| |
e |
1/5 |
| |
f |
No |
| |
g |
No |
| |
h |
See detailed notes. |
| |
|
|
| B2 |
a |
24 fish |
| |
c |
(12) 6 (2) |
| |
d |
30 fish |
| |
e |
21 fish |
| |
f |
60 fish |
| |
g |
24 fish |
| |
h |
90 fish |
| |
i |
100 fish |
| |
j |
120 fish |
| |
|
|
| B4 |
a |
21 fish |
| |
b |
25 fish |
| |
c |
30.3 = 30 fish |
| |
d |
37.5 = 38 fish |
| |
e |
16.8 = 17 fish |
| |
f |
See detailed notes. |
| |
g |
See detailed notes. |
| |
|
|
| E1 |
a |
2500 trout |
| |
|
|
| E2 |
a |
18 squirrels |
| |
c |
See detailed notes. |
| |
|
|
| E3 |
a |
50 squirrels |
| |
b |
See detailed notes. |
| |
c |
See detailed notes. |
| |
|
|
| E4 |
a |
See detailed notes. |
Page R1
| |
In the pond |
In 2nd sample |
| Marked fish |
|
|
| Fish altogether |
|
|
Table 4
| |
In the pond |
In 2nd sample |
| Marked fish |
|
|
| Fish altogether |
|
|
Table 5
| |
1st sample
(Capture) |
2nd sample |
No. of marked beads
in
2nd sample (Recapture) |
Estimate
N |
| (i) |
20 |
20 |
|
|
| (ii) |
20 |
20 |
|
|
| (iii) |
20 |
20 |
|
|
| (iv) |
20 |
20 |
|
|
| (v) |
20 |
20 |
|
|
Table 6
| |
1st sample
(Capture) |
2nd sample |
No. of marked beads
in
2nd sample (Recapture) |
Estimate
N |
| (i) |
20 |
40 |
|
|
| (ii) |
20 |
40 |
|
|
| (iii) |
20 |
40 |
|
|
| (iv) |
20 |
40 |
|
|
| (v) |
20 |
40 |
|
|
Table 7
Test Questions
- In a pond a sample of 10 fish is caught and marked, then
returned to the water. Next day a second sample of 12 is
taken, and four fish are found to be marked. Estimate how
many fish are in the pond. Give a reason why your
estimate might not be accurate.
-
- Twelve beads are taken from a bag, marked and
then returned. A second sample is taken, after
the beads have been mixed, and of 20 beads four
are marked. Estimate the number of beads in the
bag.
- Two bags each contain the same number of beads.
Ann takes a first sample of 20 from her bag,
marks them and returns them to the bag. Brian
does the same with a first sample of 40 from his
bag. They both take second samples of the same
size and estimate the number of beads. Whose
estimate is likely to be more accurate?
- From a bag containing some beads a first sample of 30 is
taken, marked and returned. Ten people come and take a
second sample of size 20. The number of marked beads in
the second samples were:
5, 6, 6, 8, 4, 5, 7, 6, 1, 3
- For each sample estimate the number of beads in
the bag.
- What are the largest and smallest estimates.
- Use all these samples to give your
estimate. Explain how you worked it out.
- Along a 400-metre stretch of river 100 fish are netted,
marked and returned to the water. A week later a second
sample of 150 is caught, and 20 are found to be marked.
Estimate how many fish are in the stretch of river. Give
any reasons why you think your estimate might be
unreliable.
- On the 1st April 1979 a trapper caught 50 rabbits in sand
dunes. He put rings round their legs to mark them. On 1st
April 1980 he caught 60 rabbits in the same place and
found that four of them had rings on. Use the capture-recapture
method to estimate the number of rabbits in the dunes on
1st April 1980. Say, with reason, whether you think this
estimate is likely to be too high or too low.
- The following table shows the results of using the
capture-recapture method to estimate the number of beads
in a bag.
| |
1st sample |
2nd sample |
No. of
marked beads
in 2nd sample |
| Alan |
40 |
20 |
12 |
| Claire |
10 |
5 |
0 |
| David |
15 |
15 |
2 |
| Elaine |
60 |
40 |
27 |
- Which estimate is likely to be nearest the
correct answer? Why?
- Which estimate is likely to be furthest from the
correct answer? Why?
Answers
| 1 |
|
30 fish. Small number of marked fish in second sample,
etc. |
| |
|
|
| 2 |
a |
60 Beads |
| |
b |
Brian's |
| |
|
|
| 3 |
a |
120, 100, 100, 75, 150, 120, 851/2
(86), 100, 600, 200 |
| |
b |
Largest 600 - Smallest 75 |
| |
c |
The mean of the other estimates which is 165. Also
acceptable is the median 110. |
| |
|
|
| 4 |
|
750 fish - marked fish go out of the stretch of water,
others enter. |
| |
|
|
| 5 |
|
750 rabbits - probably too high because of death and
migration. |
| |
|
|
| 6 |
a |
Elaine (large first sample and larger second sample). |
| |
b |
Claire (small first sample and second sample and no
marked beads in the second sample). |
Connections with Other Published Units from the Project
Other units at the Same Level (Level 3)
Car Careers
Cutting it Fine
Multiplying People
Phoney Figures
Pupil Poll
Units at Other Levels In the Same or Allied Areas of the Curriculum
Level 1
Shaking a Six
Practice makes Perfect
If at first ...
Level 2
Seeing is Believing
Getting it Right
Level 4
Smoking and Health
This unit is particularly relevant to: Science, Mathematics.
Interconnections between Concepts and Techniques Used In these Units
These are detailed in the following table. The code numbers in
the left-hand column refer to the item spelled out in more detail
in Chapter 5 of Teaching Statistics, 11-16.
An item mentioned under Statistical Prerequisites
needs to be covered before this unit is taught. Units which
introduce this idea or technique are listed alongside.
An item mentioned under Idea or Technique Used is not
specifically introduced or necessarily pointed out as such in the
unit. There may be one or more specific examples of a more
general concept. No previous experience is necessary with these
items before teaching the unit, but more practice can be obtained
before or afterwards by using the other units listed in the two
columns alongside.
An item mentioned under Idea or Technique Introduced
occurs specifically in the unit and, if a technique, there will
be specific detailed instruction for carrying it out. Further
practice and reinforcement can be carried out by using the other
units listed alongside.
| Code No. |
Statistical
Prerequisites |
Introduced in |
| 3.1c |
Mean for small data set |
Practice makes Perfect
If at first ...
Seeing is Believing
Getting it Right
Cutting it Fine |
| |
Ideas
and Techniques Used |
Introduced
in |
Also
Used in |
| 1.2a |
Using discrete data |
Seeing is Believing Pupil Poll |
Shaking a Six
Getting it Right
Multiplying People
Cutting it Fine
If at first ...
Car Careers
Phoney Figures |
| 1.3a |
Sampling from a small well-defined
population |
|
If at first .... |
| 1.4a |
Data by direct counting and measuring |
Shaking a Six |
Cutting it Fine |
| |
Ideas
and Techniques Introduced |
Also Used in |
| 1.3b |
Sampling from a large population |
Car Careers
Pupil Poll |
| 1.3e |
Variability in samples |
Practice makes Perfect
Car Careers
Smoking and Health
If at first ....
Cutting it Fine
Getting it Right
Pupil Poll |
| 1.3h |
Biased samples |
Car Careers
Pupil Poll |
| 4.3a |
Assumptions behind simple models |
Multiplying People |
| 4.3o |
Simulation as a model |
If at first ...
Multiplying People |
| 4.3p |
Setting up a simulation |
If at first ... |
| 4.3q |
Interpreting a simulation |
If at first ...
Multiplying People |
| 5a |
Reading tables |
Shaking a Six
Car Careers
Smoking and Health
If at first ...
Multiplying People
Seeing is Believing
Phoney Figures |
| 5i |
Estimating population figures from
samples |
Seeing is Believing
Smoking and Health
Getting it Right
Car Careers |
| 5k |
Variability of estimates |
Car Careers
Pupil Poll |
| 5v |
Inference from tables |
Shaking a Six
Car Careers
Phoney Figures
Practice makes Perfect
Cutting it Fine
Smoking and Health
Seeing is Believing
Multiplying People |
| 5w |
Large samples better for inference |
Shaking a Six
Getting it Right
Pupil Poll |
|